https://www.ansys.com/ko-kr/simulation-topics/what-is-computational-fluid-dynamics
전산유체역학(CFD)이란?
전산유체역학(CFD)은 컴퓨터를 사용하여 질량, 운동량 및 에너지 보존 방정식을 기반으로 액체 및 기체 흐름을 예측하는 과학입니다. 유체는 우리 주변에 있고 끊임없이 우리의 삶을 유지합니다. 성대의 진동은 말을 들을 뿐만 아니라 말을 할 수 있게 하는 공기 중의 압력파를 발생시킵니다. 유체가 없다면 테니스 공의 톱스핀은 의미가 없으며 비행기는 어떤 양력도 생성하지 못할 것입니다. CFD를 통해 우리는 세상의 거의 모든 것을 구성하는 유체를 분석, 이해 및 예측할 수 있습니다.
전산유체역학의 예
CFD는 유체 흐름 및 열 전달을 예측하거나 유체 흐름이 제품 또는 시스템에 미치는 영향을 이해하기 위해 필요한 모든 곳에서 사용됩니다. CFD는 온도, 압력, 속도 및 밀도와 같은 유체 흐름의 다양한 특성을 분석하며 다음을 포함한 산업 전반에 걸친 광범위한 엔지니어링 문제에 적용할 수 있습니다.
항공우주 및 방위: CFD를 사용하면 항공기 주변의 공기 흐름을 모델링하여 외부 공기 역학으로 알려진 양력과 항력을 예측할 수 있습니다. 이는 기업이 성능 향상과 연료 사용량 감소를 위해 항공기 설계를 최적화하려고 할 때 중요합니다. CFD는 또한 기내 공기 순환과 같은 항공기 내부의 복잡한 시스템을 시뮬레이션하여 공기 품질을 예측할 수 있습니다. 주요 응용 분야에는 항공 전자 공학 냉각, 항공 광학, 외부 공기 역학, 객실 HVAC 및 추진 장치가 포함됩니다.
자동차: 전기 모터와 배터리 전기 화학이 기계, 화학 및 전기 공학 사이의 복잡한 교차점을 이루는 전기 자동차에서 CFD를 사용하면 다중물리 시스템 전반에 걸쳐 상세한 열 연구를 수행할 수 있습니다. 이를 통해 엔지니어는 모터가 얼마나 효율적으로 냉각되는지 예측하고 화재를 일으킬 수 있는 배터리 열폭주를 줄일 수 있습니다. 주요 응용 분야로는 기어박스 윤활, 자율 센서, 공기 음향, 외부 공기 역학, 배터리 모델링 및 전기 모터 냉각이 있습니다.
새로운 에너지: 탈탄소화를 가능하게 하는 수소는 더 깨끗한 지구를 만드는 데 중요한 연료입니다. CFD를 사용하면 생산부터 저장, 운송, 소비까지 전체 수소 가치 사슬을 모델링할 수 있습니다. CFD는 탐색 연구를 수행하여 기존 엔진에서 수소 및 기타 대체 연료를 어떻게 사용할 수 있는지 알아보고 대체 연료 옵션의 효율성을 결정할 수 있습니다. 주요 응용 분야로는 PEM 전기 분해, 수소 생산, 운송, 저장 및 소비, 연료 전지 활용이 있습니다.
헬스케어: 생물의학 분야에서 CFD는 순환계를 통한 혈류, 호흡계를 통한 공기 흐름과 같은 인체 내 유체 흐름을 분석할 수 있습니다. 또한 의료 기기 개발 속도를 높이고 새로운 약물의 잠재적 효능을 평가하는 데에도 사용할 수 있습니다. 주요 응용 분야로는 심혈관 흐름, 호흡기 시스템, 바이오 의약품이 있습니다.
CFD의 지배 방정식
유체의 움직임은 고체 물체와는 매우 다르게 움직이므로 많은 사람들에게 직관적이지 않습니다. 방 안에서 공을 던지면 모양이나 질량이 변하지 않습니다. 같은 방식으로 공기를 "던질" 수 없습니다. CFD의 지배 방정식은 유체의 임의 모양과 예측할 수 없는 특성을 보상하는 데 도움이 됩니다.
클로드-루이 나비에(Claude-Louis Navier)와 조지 가브리엘 스톡스(George Gabriel Stokes)의 이름을 딴 나비에-스토크스 방정식은 유체의 운동을 설명하는 편미분 방정식입니다. 19세기 중반에 개발된 이 방정식은 유체 역학을 이해하기 위한 기본 방정식이며 날개 주변의 공기 흐름, 엔진을 통한 연료 흐름과 같은 모든 유형의 유체 흐름을 모델링하는 데 사용됩니다. 유체 거동을 모델링하기 위한 주요 지배 방정식으로 간주되며 질량, 운동량 및 에너지에 대한 보존 방정식을 기반으로 합니다.
1. 질량 보존: 연속 방정식
이 방정식은 질량 유입이나 유출이 없는 한 주어진 유체 부피의 질량이 일정하게 유지되어야 함을 나타냅니다.
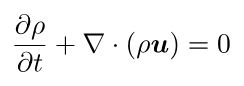
여기서 ⍴는 유체 밀도, t는 시간, u는 속도 벡터, ∇는 기울기 연산자입니다.
2. 모멘텀 보존: 뉴턴의 제2법칙
운동량 방정식은 유체 부피 내에서 운동량의 변화율이 압력과 중력을 포함하여 그 부피에 작용하는 힘의 합과 같다고 말합니다. 점도가 일정한 비압축성 유체의 경우 다음과 같이 쓸 수 있습니다.
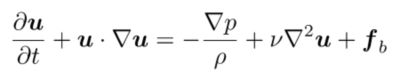
여기서 p는 정압, v는 점도, ƒb는 체적력(일반적으로 중력)입니다.
3. 에너지 보존: 열역학 제1법칙
에너지 방정식에 따르면 유체의 총 에너지 변화는 시스템에 추가되거나 시스템에서 제거(예: 전도성 또는 대류 열 전달에 의해)되는 에너지와 동일해야 합니다.

여기서 htot은 총 엔탈피, λ는 전도도, T는 온도, SE는 외부 에너지원입니다. ∇ ∙ ( u ∙ t ) 항은 점성 작업 항이며 점성 응력으로 인한 작업을 나타냅니다.
댓글 없음:
댓글 쓰기